Power Within Psychology | BLOGS

Let’s be honest — the moment you hear “p-value,” “alpha,” or “significance level” in psychology stats class, your brain either freezes… or quietly cries.
Most students think: “Is this math again?”, “Why is this even in psychology?”, or “What does this even mean and why does it sound so judgmental?”. Once you get the basic logic, it’s actually not that scary. So let’s break it down — simply, and in your language.

Let’s start from the beginning — understanding things step by step, so we know why concepts like p-value, alpha, and significance are even used in the first place, and when they actually come into play.

Usecase – Let’s Set the Foundation Before We Dive In

First comes Alpha

In any research, the researcher sets an alpha value beforehand — usually 5% because it strikes a nice balance (also more reasons are given below) — to let readers, reviewers, and other researchers know how strict they’re going to be while judging the results. It’s like setting a cutoff point to decide what’s good enough and what is not.

For example:
Let’s say at the end of this blog you feel like you’ve understood the concepts really well. Then you Think of taking a quiz with 5 multiple-choice questions to test your Understaing.

Before taking the quiz, you mentally set a rule:
“If there’s more than a 5% chance that I got these answers right just by guessing, I won’t believe I’ve truly understood.” – which means I wont allow more than 5% guesswork in my research and still call it trust worthy.

Example:
I attempt 20 MCQs and decide to set my strictness level (alpha) at 5% — meaning I’ll allow only a small chance that I got lucky.

• 5% of 20 questions = 1 question

So I’m saying:

“If more than 1 of my answers feels like a lucky guess, I won’t fully trust that I’ve understood the topic.” – that is super strict, right? And that’s how researchers want to conduct their research with little or no room for chance, guesswork, or error.

Lets look at some more points to keep in mind before we finish understanding alpha.

• Alpha is set before the research begins
  It’s a pre-decided rule, not something you adjust after seeing the results. This avoids bias.
• Researchers usually set the alpha level at 5% (0.05) as a general rule of thumb to make sure results that are worth it are considered and trusted. You might wonder why 5% and not any other number. It’s because of two reasons:
  • Higher Alpha results in Type I error – A Type I error happens when you wrongly believe your result is meaningful. If you set a higher alpha, like 10% or more, it becomes easier for random or weak results to bleed into data that is significant. That means you might treat something as unimportant, important. The higher the alpha, the more likely is for this kind of mistake can happen.
  • Alpha lower than 5% results in Type II error – This happens when you think there’s nothing there, but there actually is. Because your cutoff is so strict, you might miss real results and wrongly say they’re not significant. For example, imagine you study well and take a test, but you decide you’ll only allow yourself 1 mistake( alpha – to strict). When the results come and you made 2 mistakes, you might wrongly think, “I didn’t understand the topic,” even though you did pretty well. Because your rule was too strict, you missed a result that was actually good.
  • In short, if you reduce one type of error, the other tends to increase — so researchers set alpha at a balanced point (like 5%) to reduce the risk of both Type I and Type II errors.

Significance

Significance means the result is strong enough to trust — it happens when the p-value is smaller than alpha. Like alpha, it’s set before looking at the data to help us decide what counts as “important.” If a result has very little chance of happening by fluke, and it’s below alpha, we call it significant. Alpha and significance work together, and in most cases, they mean the same thing or are used interchangeably. Both alpha and significance work together to determine when we can reject the null hypothesis. In most cases, over 99% of the time, alpha and significance levels are identical.

There’s no fancy word for when the p-value is higher than alpha — we just say the result is insignificant (or in student terms, “bad results,” haha).

We call something significant because, “Aise result ke aane ki sambhavana chance se bahut kam thi, par fir bhi woh result aaya.— and that makes it special. For example:

You learn a topic and take a test to check your understanding.
You get 99% of the answers right — which is super rare just by luck.
Because the chances of that happening randomly are so low,
we say the result is statistically significant —
You probably didn’t just get lucky — you actually understood it.

Understanding P-Value: Your Alpha Companion

P-value by itself doesn’t mean much.
It becomes meaningful only when compared to alpha.
Without alpha, you don’t know what counts as “too much chance” —
so setting alpha gives you a clear line to judge if your result is significant or just random.

lets take the same example with and without alpha to see how it affects P-value :

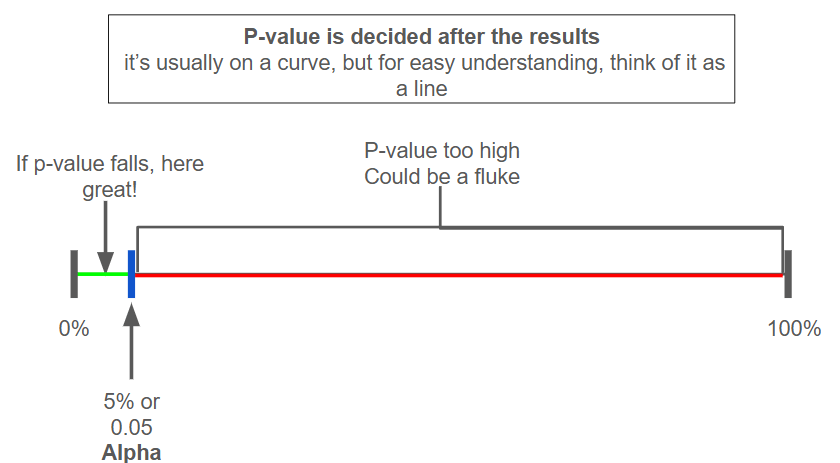
So , A low p-value means the result is probably not by chance — it’s more likely to be meaningful when lower than alpha on a scale .

To paint a better picture

• First step: Problem statment or Question is stated

• Second step: Split the Problem statement into two – Hypothesis H1 (what you believe) and the Null Hypothesis H0 (the opposite of H1). The null hypothesis is the statement we aim to prove wrong, so that the solution becomes H1( not forcefully tho).

• Third Step comes Alpha – The rule of strictness
  It’s the limit we set beforehand to decide how much chance we’re willing to accept before trusting a result.

• Fourth Step Significance is evaluated – jWhen p-value is smaller than alpha
  If the p-value falls below alpha, the result is considered statistically significant, meaning it’s unlikely to have happened by chance.

• Fifth P-value is decided – how rare the result’s probability is?
  But on its own, it doesn’t mean much — it only becomes meaningful when compared to alpha.

Here are some questions for you to solve